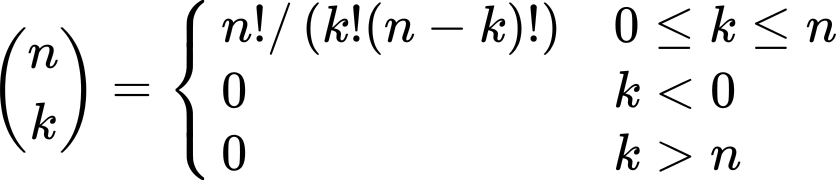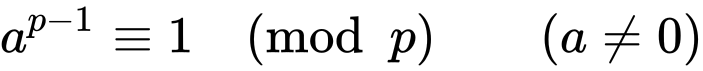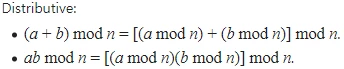백준 - 11401 이항 계수 3 풀이

문제

11401 이항 계수 3

풀이

Background

• 이항 계수[이항 계수]
  
• 페르마의 소정리[페르마의 소정리]
  

  페르마의 소정리를 이용한 ^-1 없애기
  1. a^p-1 ≡ 1 (mod p)
  2. a * a^p-2 ≡ 1 (mod p)
  3. a^p-2 ≡ 1 / a (mod p)
  4. a^p-2 ≡ a^-1 (mod p)
  5. a^-1 ≡ a^p-2 (mod p)

• 나머지 연산 속성(분배법칙)[Modulo operation]
  

  fyi
  빼기의 경우 마이너스가 될 수 있어 아래와 같이 한다.
  (a - b) mod n = [(a mod n) - (b - mod n) + n] mod n

식 정리

1. ( n! / ( k! ( n - k )! ) % p
2. = ( n! ( k! ( n - k )!)^-1 % p (페르마의 소정리)
3. = n! ( k! ( n - k )!)^p-2 % p (나머지 연산 속성)
4. = ((n! % p) (( k! ( n - k )!)^p-2 % p)) % p
5. = ((n! % p) (k!^p-2 (n - k)!^p-2) % p) % p
6. = ((n! % p) (k!^p-2 % p) ((n - k)!^p-2 % p)) % p

답

kotlin code

fun main() {
    println(Long.MAX_VALUE)
    println(1000000006 * 1000000006)
    println(1000000006L * 1000000006L)
    println(Int.MAX_VALUE.toLong() * Int.MAX_VALUE.toLong())
    q11401()
}

fun q11401() {
    val input = readln().split(" ").map { it.toInt() }
    val n = input.first()
    val k = input.last()
    val p = 1000000007

    val nFactorialModP = factorialModP(n, p)
    val kFactorialPowerPMinusTwoModP = powerModP(factorialModP(k, p), p-2, p)
    val nMinusKFactorialPowerPMinusTwoModP = powerModP(factorialModP(n-k, p), p-2, p)

    println(nFactorialModP.toBigDecimal().multiply(kFactorialPowerPMinusTwoModP).multiply(nMinusKFactorialPowerPMinusTwoModP).remainder(p))
}

private tailrec fun factorialModP(n:Int, p:Int, acc:Int = 1): Int = when(n) {
    0 -> acc % p
    else -> factorialModP(n-1, p, ((acc.toLong() * n.toLong()) % p).toInt())
}

private fun powerModP(a: Int, b: Int, p: Int): Int = when {
    b == 0 -> 1
    b.isOdd() -> {
        val half = (powerModP(a,b/2, p) % p).toLong()
        ((half * half) % p).toInt()
    }
    else -> ((a.toLong() * powerModP(a,b-1, p).toLong()) % p).toInt()
}

private fun Int.toBigDecimal(): java.math.BigDecimal {
    return java.math.BigDecimal.valueOf(this.toLong())
}

private fun java.math.BigDecimal.multiply(multiplicand: Int): java.math.BigDecimal {
    return this.multiply(multiplicand.toBigDecimal())
}

private fun java.math.BigDecimal.remainder(divisor: Int): java.math.BigDecimal {
    return this.remainder(divisor.toBigDecimal())
}

private fun Int.isOdd(): Boolean {
    return this % 2 == 0
}