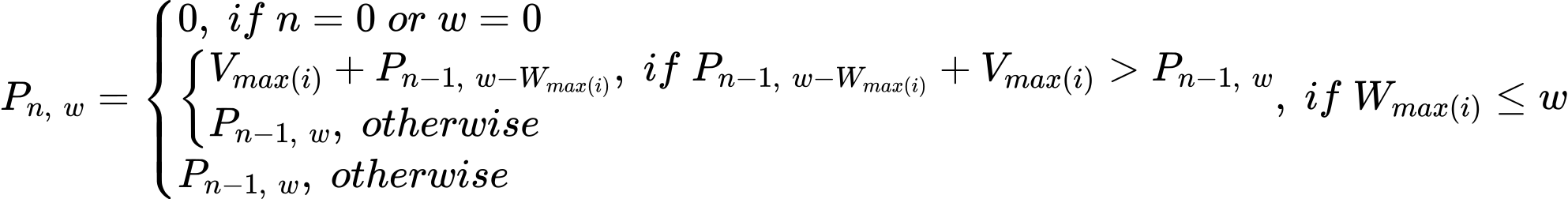백준 - 12865 평범한 배낭 풀이

문제

12865 평범한 배낭

풀이

1. 알고 있어야 할 점

• 다이나믹 프로그래밍을 이용한다.
  • 동적 계획법(動的計劃法, dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다.[동적 계획법]
  • 수식 $\newline n:\;담을\,수\,있는\,물건의\,수(담을\,수\,있는\,물건의\,번호:\,0 \leq i \leq n-1)$
    $w:\;버틸\,수\,있는\,무게$
    $i:\;물건의\,번호$
    $max(i): 담을\,수\,있는\,물건의\,번호\,중\,최댓값(max(i) = n-1)$
    $P_{n,\;w}:\;n개의\,물건을\,담을\,수\,있고,\,버틸\,수\,있는\,무게가\,w인\,배낭에\,넣을\,수\,있는\,물건들의\,가치합의\,최댓값$
    $V_i:\;i\,물건이\,가치$
    $W_i:\;i\,물건의\,무게$
    
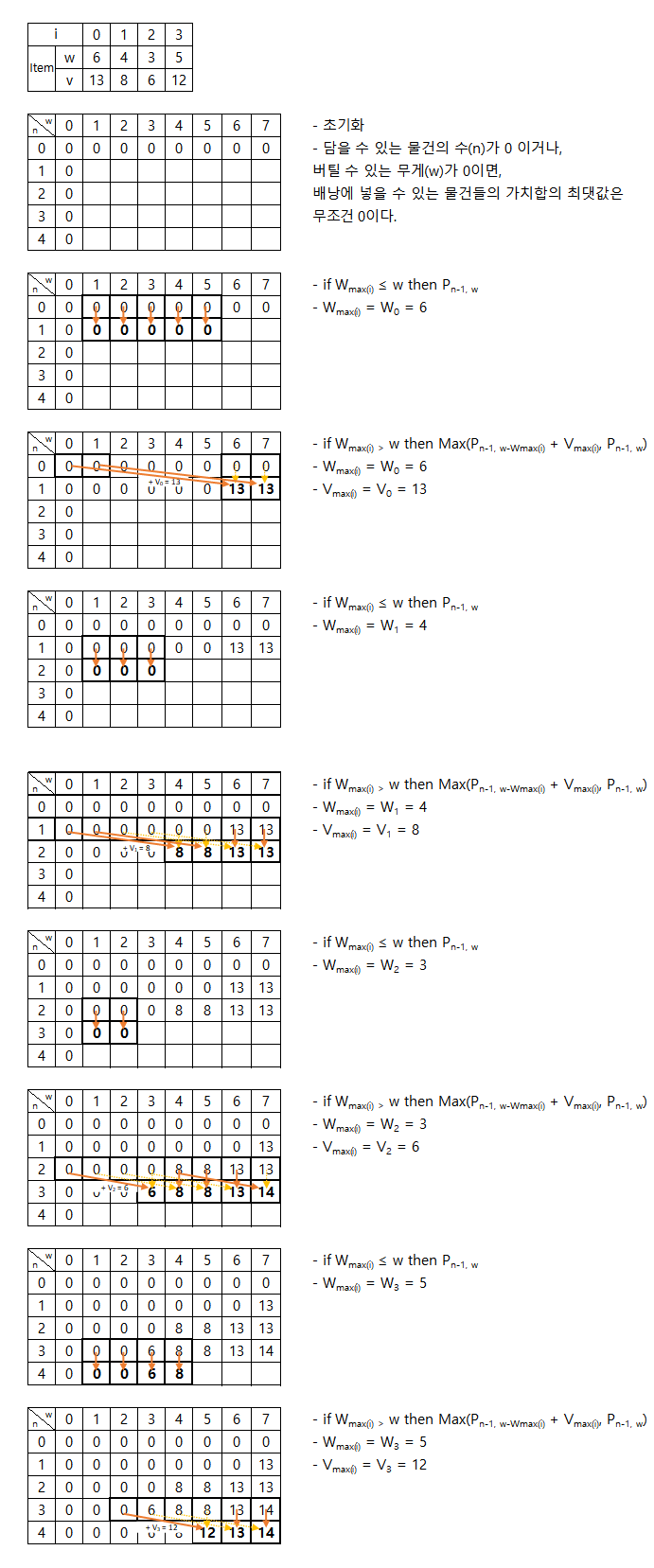
• 문제의 예제 1의 연산 과정
• 

2. Step by Step

재귀를 사용하는 방법(timeout 발생)

1. 입력을 받는다.

• code ```kotlin val (numOfItems, maxWeight) = readln().split(“ “).map { it.toInt() } val items = Array(numOfItems) { readln().split(“ “).let { Item(it.first().toInt(), it.last().toInt()) } }

data class Item(val w: Int, val v: Int)

#### 2. 수식을 재귀 함수로 작성한다.
- code
```kotlin
fun p(n: Int, w: Int, items: Array<Item>): Int = when {
    n == 0 || w == 0 -> 0
    items[n-1].w <= w -> kotlin.math.max(p(n-1, w-items[n-1].w, items) + items[n-1].v, p(n-1, w, items))
    else -> p(n-1, w, items)
}

3. 결과 값을 출력한다.

• code

  println(p(numOfItems, maxWeight, items))
  

반복문을 사용하는 방법

1. 입력을 받는다.

• code ```kotlin val (numOfItems, maxWeight) = readln().split(“ “).map { it.toInt() } val items = Array(numOfItems) { readln().split(“ “).let { Item(it.first().toInt(), it.last().toInt()) } }

data class Item(val w: Int, val v: Int)

### 2. 가치합의 최댓값 저장할 변수를 선언한다.
- 정수형 2차원 배열을 이용한다.
- 배열의 각 값은 0으로 초기화 한다.
- code
```kotlin
val p = Array(numOfItems + 1) { IntArray(maxWeight + 1) { 0 } }

2. 수식을 반복문으로 작성한다.

• 배열을 0으로 초기화 하였기 때문에 n=0, w=0인 경우에 대해서는 이미 0이 입력되어 있다.
• 그러므로, 1부터 반복문을 시작한다.
• code

  for(n in (1..numOfItems)) {
    for(w in (1..maxWeight)) {
        val item = items[n-1]
        p[n][w] = if(w >= item.w) kotlin.math.max(p[n-1][w-item.w] + item.v, p[n-1][w]) else p[n-1][w]
    }
  }
  

3. 결과 값을 출력한다.

• code

  println(p(numOfItems, maxWeight, items))
  

답

kotlin code: 재귀를 사용하는 방법(timeout 발생)

fun main() {
    val (numOfItems, maxWeight) = readln().split(" ").map { it.toInt() }
    val items = Array(numOfItems) { readln().split(" ").let { Item(it.first().toInt(), it.last().toInt()) } }

    println(p(numOfItems, maxWeight, items))
}

data class Item(val w: Int, val v: Int)

private fun p(n: Int, w: Int, items: Array<Item>): Int = when {
    n == 0 || w == 0 -> 0
    items[n-1].w <= w -> kotlin.math.max(p(n-1, w-items[n-1].w, items) + items[n-1].v, p(n-1, w, items))
    else -> p(n-1, w, items)
}

kotlin code: 반복문을 사용하는 방법

fun main() {
    val (numOfItems, maxWeight) = readln().split(" ").map { it.toInt() }
    val items = Array(numOfItems) { readln().split(" ").let { Item(it.first().toInt(), it.last().toInt()) } }

    println(p(numOfItems, maxWeight, items))
}

data class Item(val w: Int, val v: Int)

private fun p(numOfItems: Int, maxWeight: Int, items: Array<Item>): Int {
    val p = Array(numOfItems + 1) { IntArray(maxWeight + 1) { 0 } }

    for (n in (1..numOfItems)) {
        for (w in (1..maxWeight)) {
            val item = items[n - 1]
            p[n][w] = if (w >= item.w) max(p[n - 1][w - item.w] + item.v, p[n - 1][w]) else p[n - 1][w]
        }
    }
    
    return p.last().last()
}

Reference

• 동적 계획법

Attachments

• 이미지 원본