백준 - 1753 최단경로 풀이

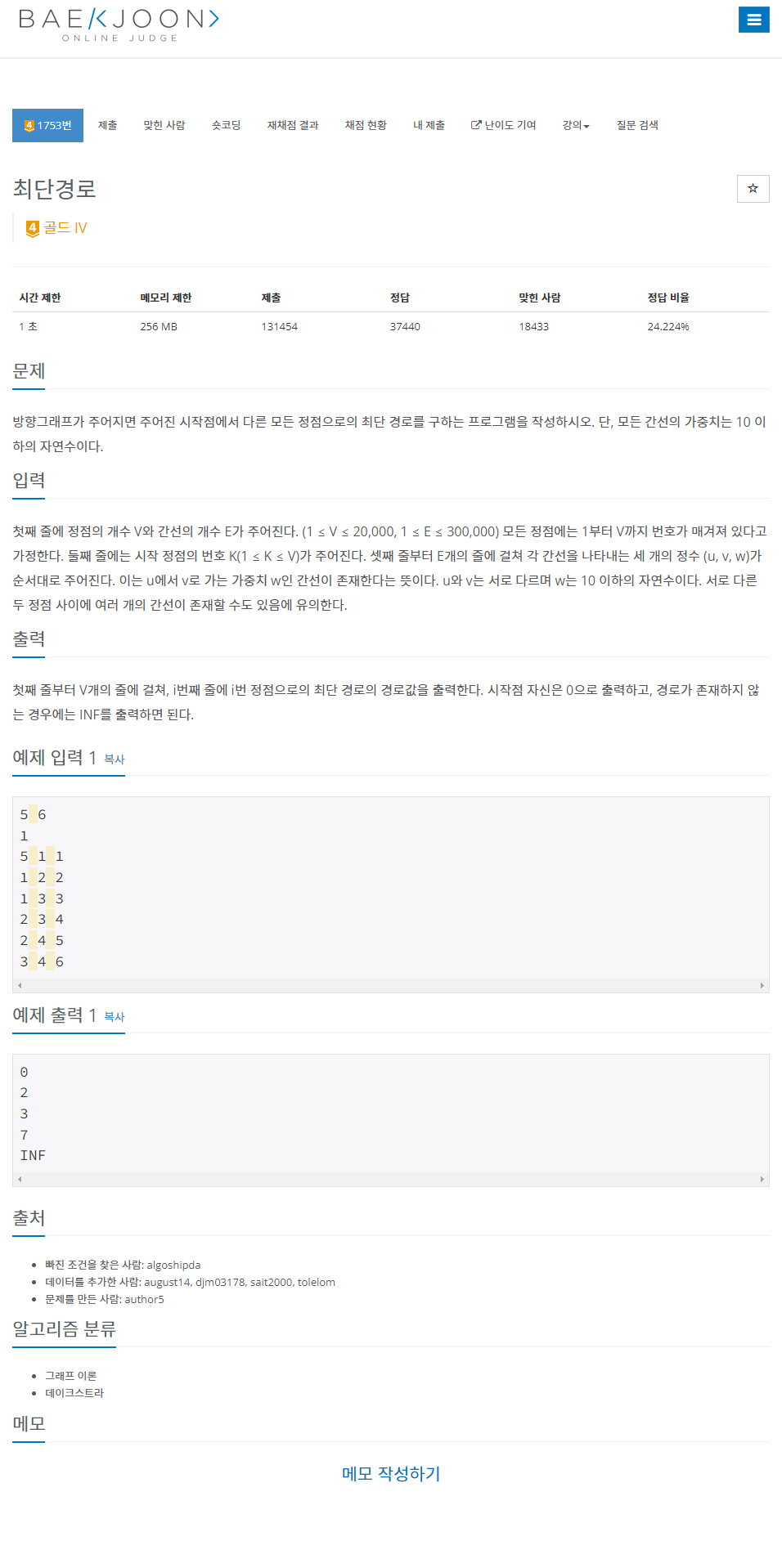
문제

1753 최단경로

풀이

1. 알고 있어야 할 점

• 이 문제는 전형적인 데이크스트라 알고리즘을 이용하여 푸는 문제이다.

2. 문제의 예제 1의 연산 과정

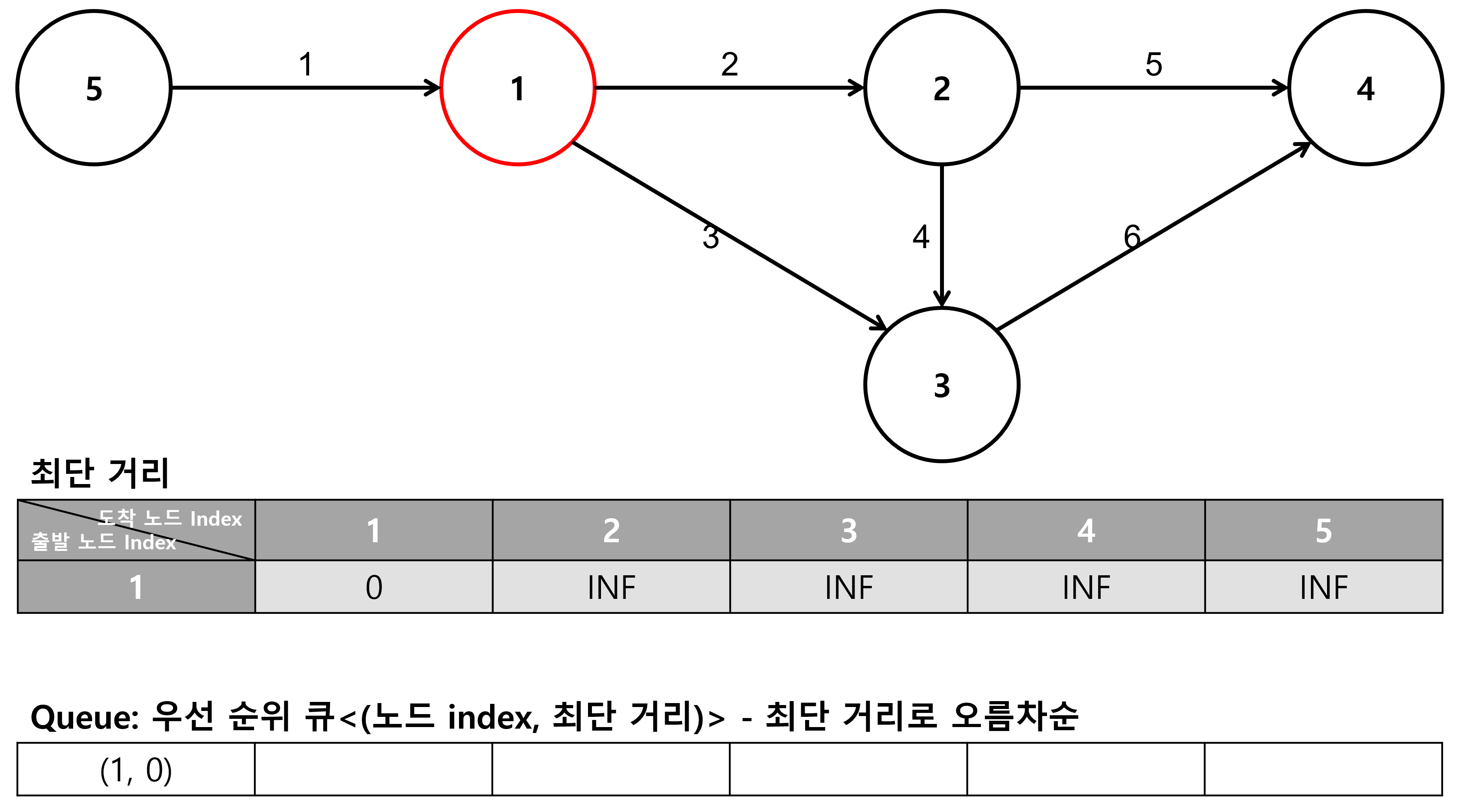
1. 시작 노드인 1로 초기화

• 노드 1에서 노드 1은 같은 노드이므로 최단 거리가 0이다.
• 우선 순위 큐를 선언하고, 노드 0를 넣는다.

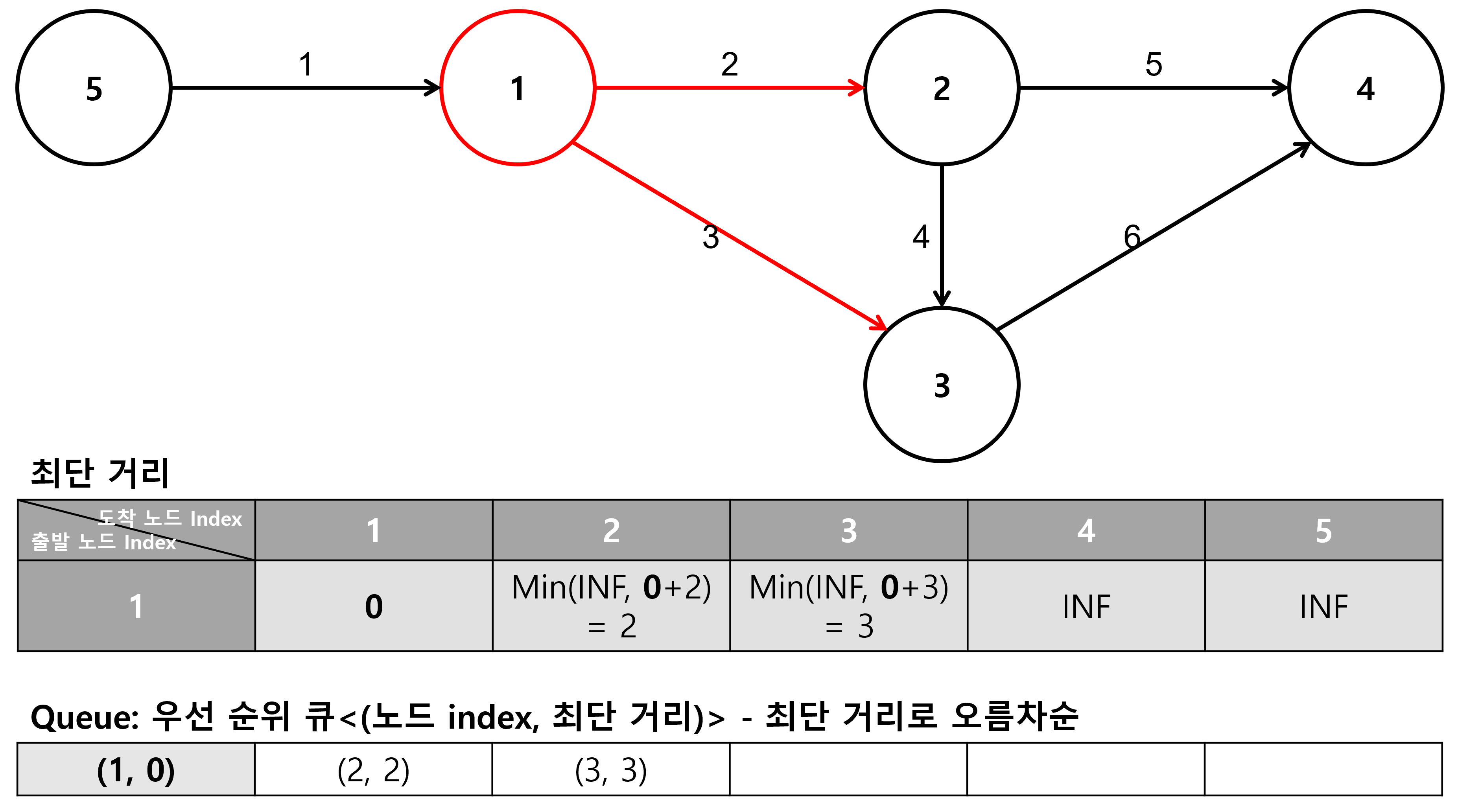
2. 노드 1에서 탐색

• 노드 1에서 노드 2까지의 최단 거리는 노드 1에서 노드 1까지의 최단 거리인 0과 노드 1에서 노드 2까지의 거리인 2의 합인 2이다.
• 노드 2의 최단 거리를 갱신하고, 큐에 노드 2를 넣는다.
• 노드 1에서 노드 3까지의 최단 거리는 노드 1에서 노드 1까지의 최단 거리인 0과 노드 1에서 노드 3까지의 거리인 3의 합인 3이다.
• 노드 3의 최단 거리를 갱신하고, 큐에 노드 3를 넣는다.

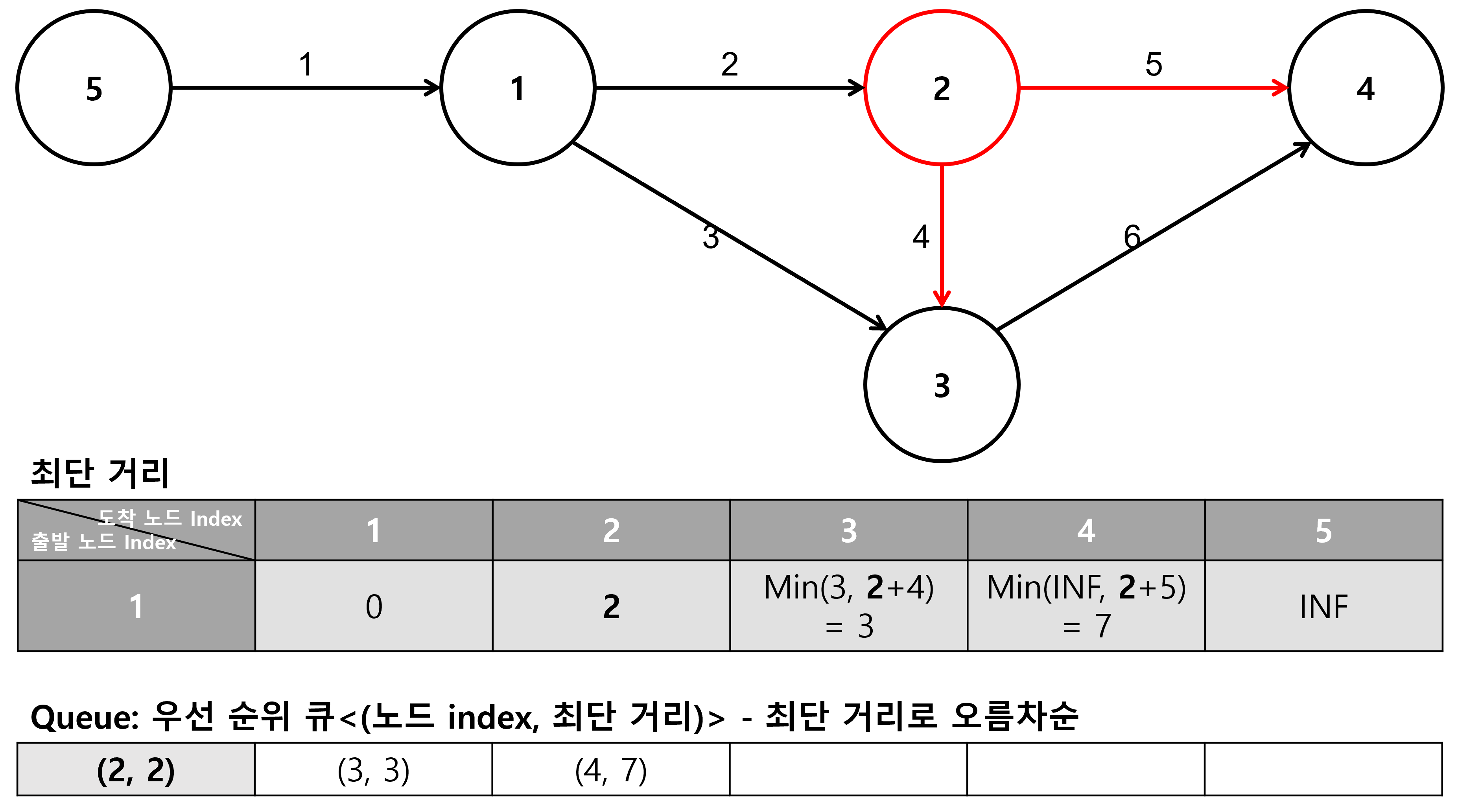
3. 노드 2에서 탐색

• 큐에 들어있는 노드 중 노드 2의 최단 거리가 가장 짧으므로 노드 2를 가져온다.
• 노드 1에서 노드 3까지의 최단 거리는 기존에 계산한 최단 거리인 3이 노드 1에서 노드 2까지의 최단 거리인 2와 노드 2에서 노드 3까지의 거리인 4의 합인 6보다 짧으므로 3이다.
• 노드 3은 최단 거리 생신이 필요 없으므로, 추가 작업 없이 다음으로 넘어간다.
• 노드 1에서 노드 4까지의 최단 거리는 노드 1에서 노드 2까지의 최단 거리인 2와 노드 2에서 노드 4까지의 거리인 5의 합인 7이다.
• 노드 4의 최단 거리를 갱신하고, 큐에 노드 4를 넣는다.

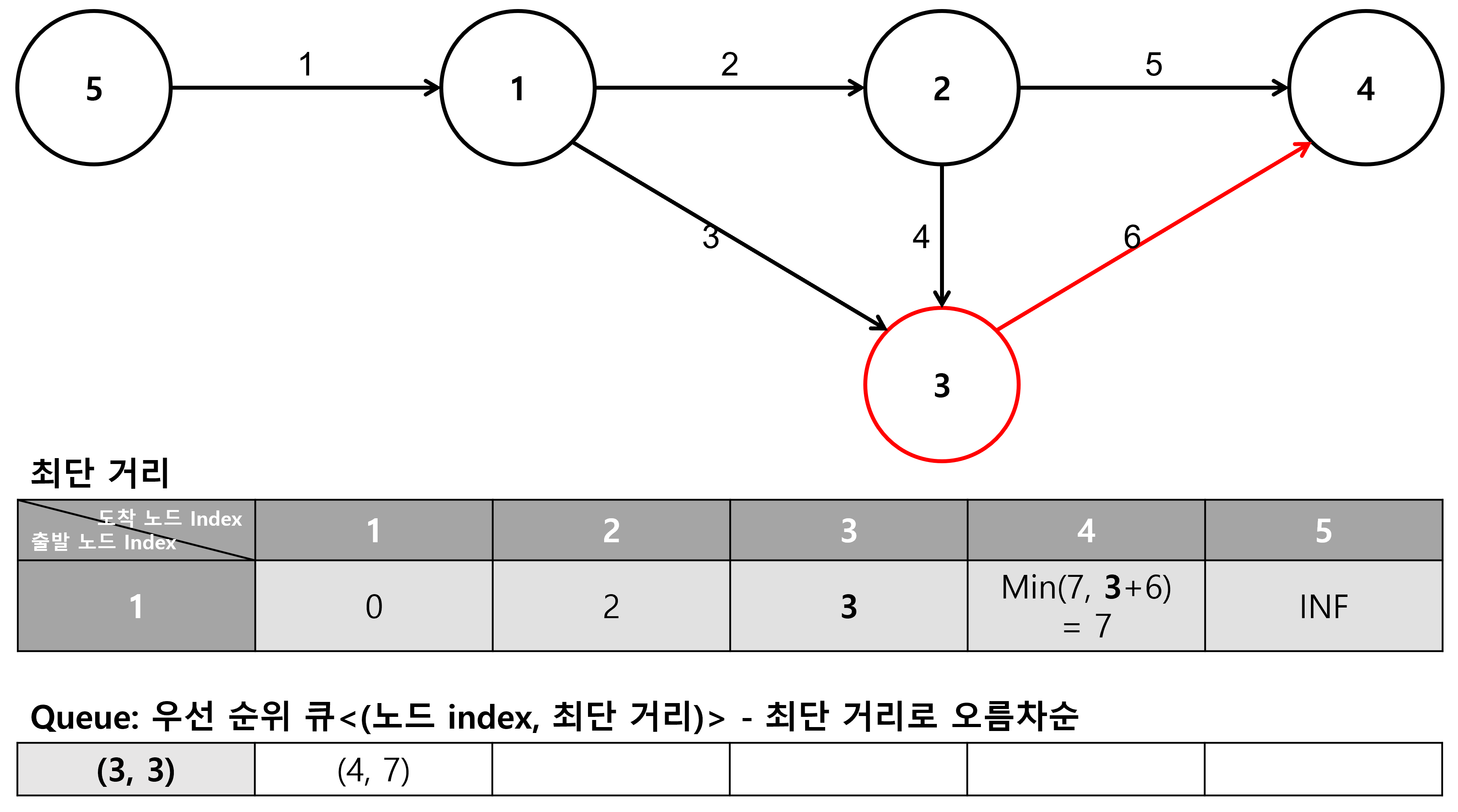
4. 노드 3에서 탐색

• 큐에 들어있는 노드 중 노드 3의 최단 거리가 가장 짧으므로 노드 3을 가져온다.
• 노드 1에서 노드 4까지의 최단 거리는 기존에 계산한 최단 거리인 7이 노드 1에서 노드 3까지의 최단 거리인 3와 노드 3에서 노드 4까지의 거리인 6의 합인 9보다 짧으므로 7이다.
• 노드 4은 최단 거리 생신이 필요 없으므로, 추가 작업 없이 다음으로 넘어간다.

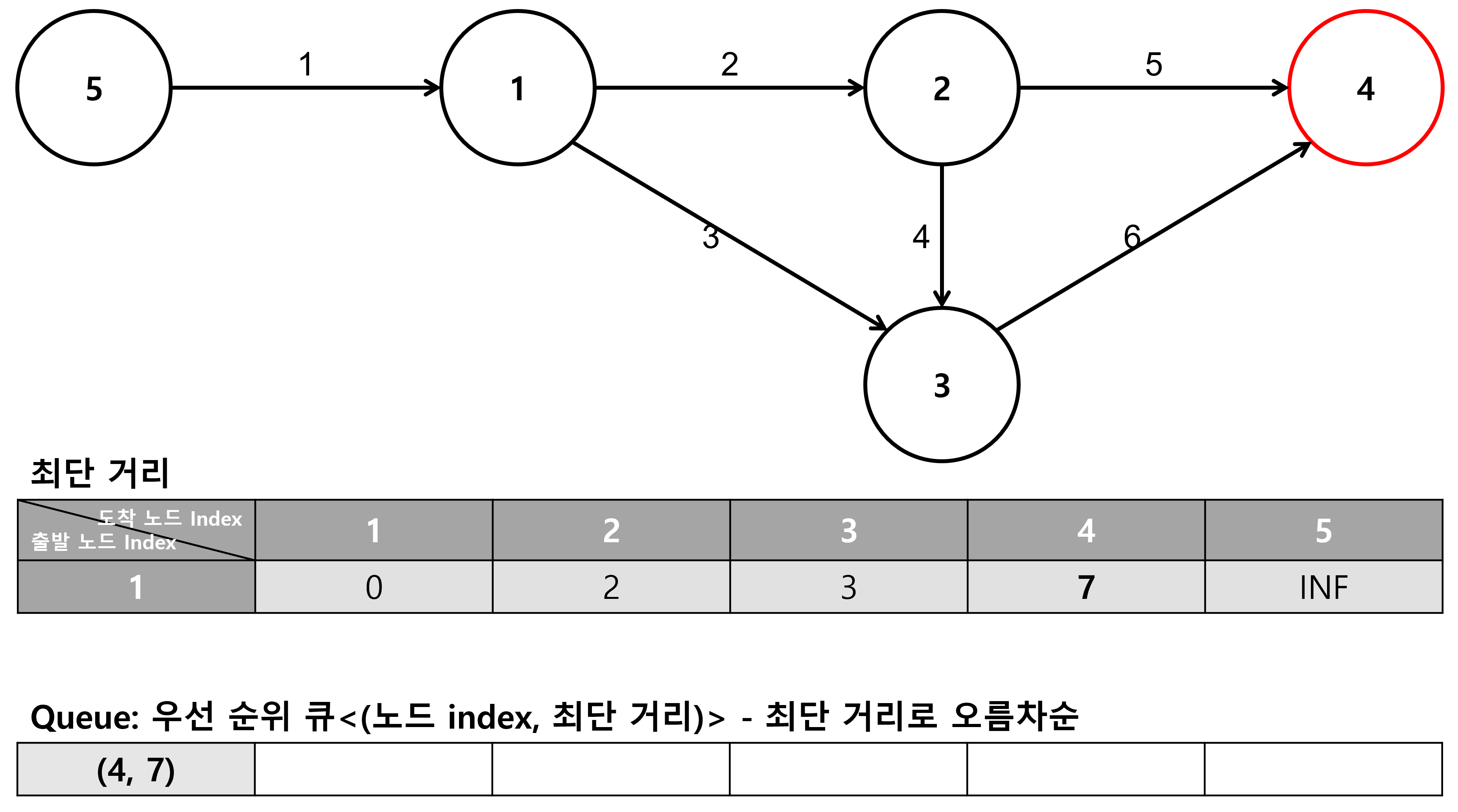
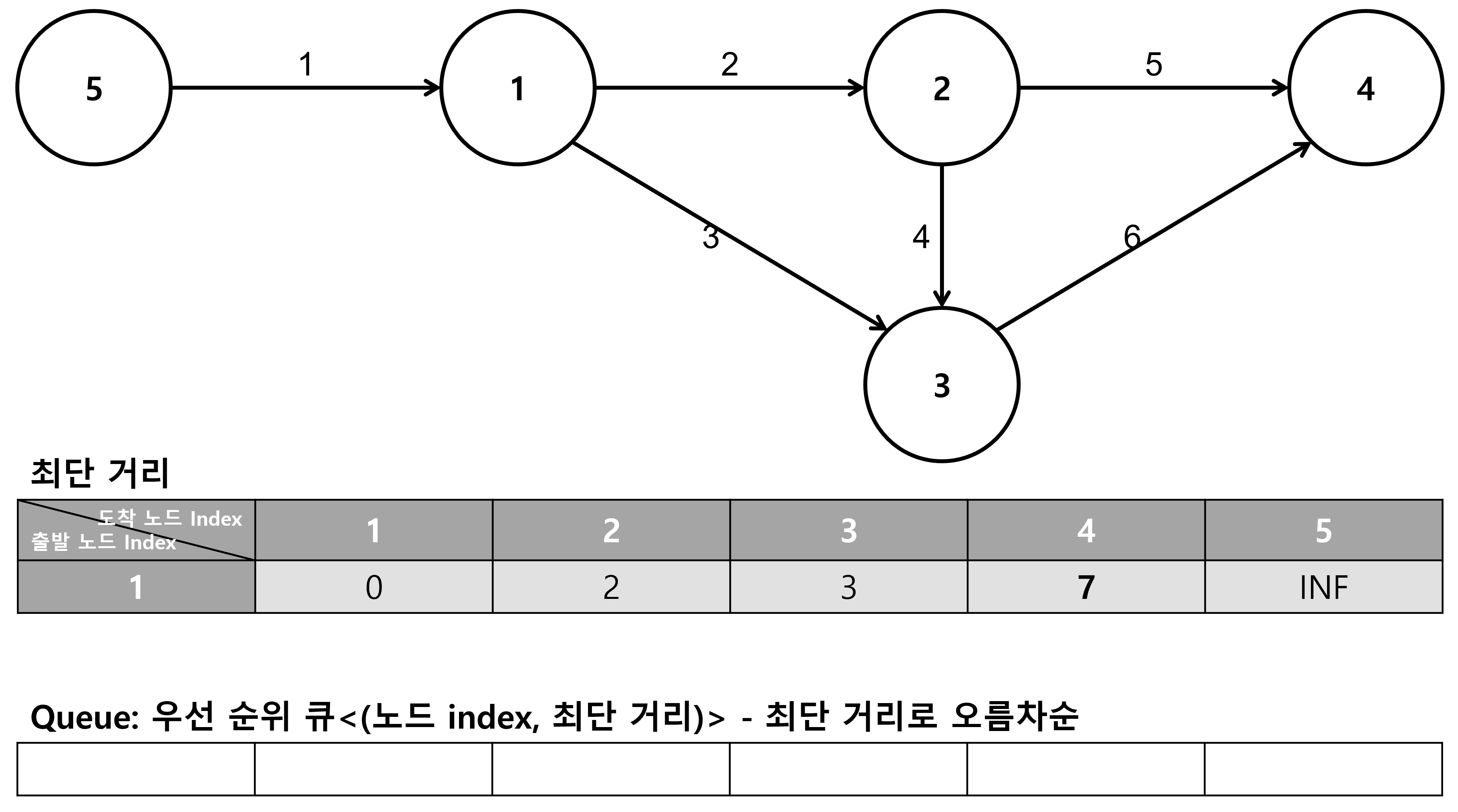
5. 노드 4에서 탐색

• 큐에 들어있는 노드 중 노드 4의 최단 거리가 가장 짧으므로 노드 4을 가져온다.
• 노드 4에서 갈 수 있는 노드가 없으므로, 추가 작업 없이 다음으로 넘어간다.

6. 종료

• 큐에서 들고올 값이 없으므로(큐가 비었으므로) 알고리즘을 종료한다.

Step by Step

1. 초기화

• 경로를 시작 노드(u)를 key로 하는 map으로 입력 받는다.
  • 경로의 경우 로직에서 반복문을 돌면서 계속 시작 노드(u)에서 도착 노드(v)를 찾는 과정이 반복도어 O(n^2)의 시간 복잡도가 발생한다. 그러므로 시간 복잡도를 줄이기 위해 맵으로 받는다.(배열 탐색(O(n)) –> 맵 탐색(O(1)))
• 최단 거리를 저장하기 위한 크기가 노드의 수인 1차원 배열을 생성하고 INF(무한대( 충분히 큰 수))로 초기화 한다.
• 시작 노드에서 시작 노드까지의 최단 거리는 0이므로 배열의 시작 노드 위치에 0을 입력한다.
• 큐에 시작 노드를 입력한다.

2. 큐에서 최단 거리가 가장 짧은 노드를 가져온다.

3. 가져온 노드에서 갈 수 있는 노드들의 최단 거리를 구한다.

• 기존 최단 거리: 기존에 구한 해당 시작 노드에서 해당 노드까지의 최단 거리
  • 시작 노드에서 해당 노드까지의 최단 거리를 연산 전이라면 기존 최단 거리는 1번 과장에서 INF로 초기화를 하였으므로 INF이다.
• 새로 계산한 최단 거리: 시작 노드에서 가져온 노드까지의 최단 거리 + 가져온 노트에서 해당 노드의 거리
• 최단 거리는 기존 최단 거리와 새로 계산한 최단 거리 중 더 작은 값이다.

4. 최단 거리를 갱신한 노드를 큐에 입력한다.

5. 큐가 빌때까지 2~4 과정을 반복한다.

답

kotlin code

const val INF = Int.MAX_VALUE

fun main() {
    val (v, e) = readln().split(' ').map { it.toInt() }
    val k = readln().toInt() - 1
    val pathMap = Array(e){ readln().split(' ').map { it.toInt() }.let { intArrayOf(it[0]-1, it[1]-1, it[2]) } }.groupBy ({ it.first() }, { Line(it[1], it[2]) })

    val nodes = getShortestPath(v, k, pathMap)

    nodes.print()
}

private fun Array<Node>.print() {
    println(java.lang.StringBuilder().let { sb ->
        this.forEach {
            sb.append(if (it.distance == INF) "INF" else it.distance).append('\n')
        }
        sb
    })
}

private fun getShortestPath(v: Int, k: Int, pathMap: Map<Int, List<Line>>): Array<Node> {
    val nodes = Array(v) { Node(it) }
    val nodesToVisitQueue = java.util.PriorityQueue<Node>()

    k.let {
        nodes[it].distance = 0
        nodesToVisitQueue.offer(nodes[it])
    }

    while (nodesToVisitQueue.isNotEmpty()) {
        val currNode = nodesToVisitQueue.poll()
        if (!pathMap.containsKey(currNode.index)) continue
        for (pathFromCurrNode in pathMap[currNode.index]!!) {
            val newDistance = currNode.distance + pathFromCurrNode.weight

            if (nodes[pathFromCurrNode.destNodeIndex].distance > newDistance) {
                nodes[pathFromCurrNode.destNodeIndex].distance = newDistance
                nodesToVisitQueue.offer(nodes[pathFromCurrNode.destNodeIndex])
            }
        }
    }

    return nodes
}

data class Line(val destNodeIndex: Int, val weight: Int)

data class Node(val index: Int, var distance: Int = INF) : Comparable<Node> {
    override fun compareTo(other: Node): Int = distance-other.distance
}

Reference

• 데이크스트라 알고리즘

Attachments

• 이미지 원본