백준 - 9663 N-Queen 풀이

문제

9663 N-Queen

풀이

1. 알고 있어야 할 점

• 퀸은 가로, 세로, 대각선으로 이동한다.

  

2. 설계

• 체스판을 2차원 배열로 생각하기 쉽지만, 한 줄에 퀸이 1개만 가능하기 때문에 1차원 배열로 표현가능한다.
• 이 문제는 시간과 메모리 제한이 있기때문에 1차원 배열로 사용해야 한다.
• 1차원 배열에 값을 표현하면 배열의 인덱스는 세로위치, 배열의 값은 가로위치가 된다.
  • 가로, 세로를 반대로 생각하여도 상관없다.

  

• 한 줄씩 가능한 위치에 퀸을 배치하며 경우의 수를 찾는다.

3. Step by Step

1. 퀸 배치

• 알고리즘

  1. 입력 받은 수가 N이라면, 사이즈가 N(인덱스: 0..N-1)인 1차원 배열을 생성하고 0에서 N-1까지의 value 입력을 시작한다.
  2. 배열의 첫 index(0)에 첫 value(0)을 입력한다.
  3. 배열에 입력한 value가 유효한지(해당 자리에 퀸을 놓을 수 있는지) 확인 한다.
     • 유효하다면 배열의 다음 index에 valuse를 다시 0부터 입력한다.
     • 유효하지 않다면, 다음 value를 입력한다.
  4. 위의 과정을 반복한다
  5. 배열이 가득 차면 경우의 수에 1을 더한다.

• code

  fun setQueen(board: IntArray, currIndex: Int, n: Int): Int = when(currIndex) {
    n -> 1
    else -> {
        var output = 0
        for(i in (0 until n)) {
            board[currIndex] = i
            if(isAvailable(board, currIndex)) output += setQueen(board, currIndex+1, n)
        }
        output
    }
  }
  

2. 해당 자리가 유효한지(퀸을 놓을 수 있는지) 확인

• 하나의 세로줄(index)에 하나의 퀸만 존재 가능한다
  • 하나의 index에 하나의 value만 가질 수 있다.
  • 기본 전제로, 1차원 배열을 사용하기 때문에 확인이 필요 없다.
• 하나의 가로줄(value)에 하나의 퀸만 존재 가능하다.
  • 즉, 새로운 퀸은 기존 퀸과 같은 value를 가질 수 없다.
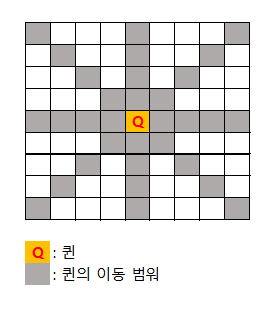
• 대각선 상에 하나의 퀸만 존재 가능하다.
  • 즉, 새로운 퀸과 기존 퀸의 value 차의 절대값은 새로운 퀸과 기존 퀸의 index 차와 동일 할 수 없다.
    • 새로운 퀸의 index는 언제나 기존 퀸의 index보다 크기 때문에 새로운 퀸과 기존 퀸의 인덱스 차는 항상 양수이다.
    • 대각선은 새로운 퀸이 기존 퀸의 우하단에 위치할 경우와 우상단에 위치할 경우가 존재한다.
    • 대각선은 새로운 퀸이 기존 퀸의 우하단에 위치할 경우 새로운 퀸과 기존 퀸의 value 차이 는 양수이고, 우상단에 위치할 경우 새로운 퀸과 기존 퀸의 value 차이 는 음수이다.
• code

  fun isAvailable(board: IntArray, currIndex: Int): Boolean {
    for(i in (0 until currIndex)) when(board[currIndex]-board[i]) {
        0, (currIndex-i), -(currIndex-i) -> return false
    }
    return true
  }
  

3. 최적화

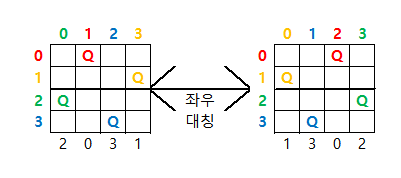
• 퀸의 배치 경우는 좌우 대칭이다.

  

• 즉, index가 0인 지점의 value은 (0 until n)이 아닌 (0 until n/2)만 대입하여, 경우의 수를 구한 후 2배를 하여도 된다.

• n이 홀수일 경우 index가 0인 지점에 value가 중앙(n / 2 + 1)인 경우의 경우의 수를 추가로 더하여야 한다.

• code

  private fun setQueenOptimization(n: Int): Int {
    val board = IntArray(n) { n / 2 }
    var output = if (n % 2 != 0) setQueen(board, 1, n) else 0
    for (value in (0 until n / 2)) {
        board[0] = value
        output += (setQueen(board, 1, value) * 2)
    }
    return output
  }
  

답

kotlin code

fun main() = println(setQueenOptimization(readln().toInt()))

private fun setQueenOptimization(n: Int): Int {
    val board = IntArray(n) { n / 2 }
    var output = if (n % 2 != 0) setQueen(board, 1, n) else 0
    for (value in (0 until n / 2)) {
        board[0] = value
        output += (setQueen(board, 1, value) * 2)
    }
    return output
}

fun setQueen(board: IntArray, currIndex: Int, n: Int): Int = when(currIndex) {
    n -> 1
    else -> {
        var output = 0
        for(i in (0 until n)) {
            board[currIndex] = i
            if(isAvailable(board, currIndex)) output += setQueen(board, currIndex+1, n)
        }
        output
    }
}

fun isAvailable(board: IntArray, currIndex: Int): Boolean {
    for(y in (0 until currIndex)) when(board[currIndex]-board[y]) {
        0, (currIndex-y), -(currIndex-y) -> return false
    }
    return true
}

Attachments

• 이미지 원본