코틀린으로 배우는 함수형 프로그래밍 - 8장 애플리케이티브 펑터

Posted Jul 16, 2022

By June 33 min read

범위

8장 애플리케이티브 펑터

개념 정리

애플리케이티브 스타일 프로그래밍(applicative style programming): 컨텍스트를 유지한 상태에서 함수에 의한 연속적인 데이터 변환을 체이닝하는 방식.
이더(either): 성공과 실패를 모두 포함하는 컨텍스트. 성공한 경우는 라이트가 되고, 실패한 경우는 레프트가 된다. 두 상태는 각각 다른 타입을 포함할 수 있기 때문에 이더의 타입 매개변수는 두 개다.

책에서 기억하고 싶은 내용

애플리케이티브 펑터는 펑터가 가진 한계 때문에 등장하였다.
펑터의 한계: 이러한 펑터의 한계를 극복하기 위해 필요한 것이 애플리케이티브 펑터다.
- 펑터는 일반적인 함수(transform: (A) → B)로만 매핑이 가능하기 때문에, 펑터를 입력으로 넣을 수 없다.
- 펑터는 함수를 포함할 때, 일반 값이 아닌 또 다른 펑터 내의 값을 적용하려면 상당히 복잡한 과정을 거쳐야 한다.
- 함수를 가진 펑터는 다른 펑터의 값을 적용해야 할 때, 컨텍스트 안에서 처리하는 것이 불가능한다.
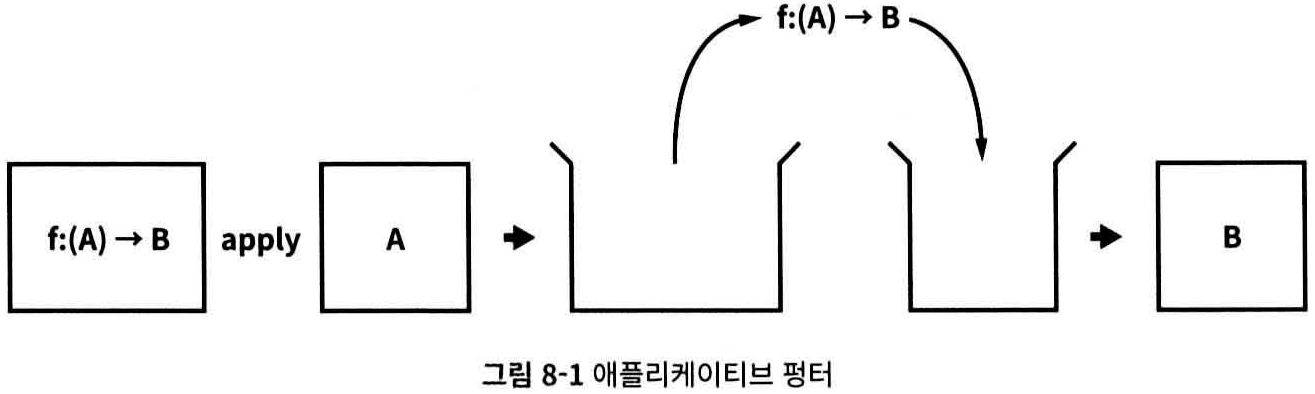
애플리케이티브 펑터는 첫 번째 상자에 담겨 있는 함수와 두 번째 상자에 담겨있는 값을 꺼내서 매핑하고, 다시 상자 안에 넣어서 반환한다.

기본적으로 애플리케이티브는 펑터의 확장판이다. 따라서 Functor를 상속하고 있고, fmap 함수를 사용할 수 있다.
- fmap 함수는 일반적인 함수를 받아서 펑터안에 값을 적용하고 다시 펑터에 넣어서 반환한다.
애플리케이티브에는 pure 함수와 apply 함수가 있다.
- pure 함수는 임의이 값을 입력으로 받아서 애플리케이티브 안에 그대로 넣고 반환한다. 이때 반환된 애플리케이티브 펑터는 최소한의 컨텍스트다. 최소한의 컨텍스트는 입력된 값만 포함된 상태의 애플리케이티브 펑터이다. pure 함수는 어떤 값을 받아서 가공 없이 그래도 상자에 포장하는 것으로 비유할 수 있다.
- apply 함수는 함수를 가진 애플리케이티브를 입력으로 받아서 펑터 안의 값을 함수에 적용하고, 적용한 결괏값을 애플리케이티브에 넣어서 반환한다.
애플리케이티브 펑터의 법칙
- 항등(identity) 법칙
  - 표현식: pure(identity) apply af = af
    - fun identity() = { x:Int → x }
  - 항등 함수에 값을 적용하는 것 외에는 아무것도 하지 않는다. 따라서 아무것도 하지 않고 그대로 af를 반환한다.
- 합성(composition) 법칙
  - 표현식: pure(compose) apply af1 apply af2 apply af3 = af1 apply (af2 apply af3)
    - fun <P1, P2, P3> compose() = { f: (P2) → P3, g: (P1) → P2, v: P1 → f(g(v)) }
    - pure 함수에 compose 함수를 넣으려면 입력과 출력이 한 개인 함수의 체인으로 커링해야 한다.
    - 좌변은 pure를 사용해서 애플리케이티브 펑터에 합성함수 compose를 넣고, 애플리케이티브 펑터 af1과 af2와 af3을 적용한 걸 의미한다.
    - 우변은 애플리케이티브 펑터 af2에 af3를 적용한 애플리케이티브 펑터를 af1에 적용한 걸 의미한다.
    - 이 좌변과 우변의 결과가 같아야 한다.
- 준동형 사상(homomorphism) 법칙
  - 표현식: pure(function) apply pure(x) = pure(function(x))
    - 좌변은 pure를 사용해서 함수 function과 값 x를 애플리케이티브 펑터에 넣는 걸 의미한다.
    - 우변은 function 함수에 x 값을 적용한 function(x)를 애플리케이티브 펑터에 넣는 걸 의미한다.
    - 이 좌변과 우변의 결과가 같아야 한다.
- 교환(interchange) 법칙
  - 표현식: af apply pure(x) = pure(of(x)) apply af
    - fun <T, R> of(value: T) = { f: (T) → R → f(value) }
      - of는 x를 다른 함수의 매개변수로 제공하는 함수다.
      - of 함수는 value를 적용할 함수를 만들 수 있다.
      - of 함수는 함수가 아닌 값 x를 미래에 적용될 함수로 만들어 줌으로써 apply의 좌변에 있는 pure 함수의 입력으로 넣을 수 있게 한다.
    - 좌변은 어떤 함수를 포함한 애플리케이티브 펑터 af와 값 x를 넣은 애플리케이티브 펑터를 적용하는 걸 의미한다.
    - 우변은 of(x)를 애플리케이티브 펑터에 넣어서 af에 적용하는 걸 의미한다.
    - 이 좌변과 우변의 결과가 같아야 한다.
펑터와 애플리케이티브 펑터 간의 관계 법칙
- pure(function) apply af = af.fmap(function)
애플리케이티브 펑터의 법칙들은 모두 카테고리 이론(category theory)라는 수학을 기반으로 한다.
- 각 법칙은 수학적으로 증명된 이론들이기 때문에 법칙들을 만족하는 펑터와 애플리케이티브 펑터들은 항상 기대한 동작을 한다는 것을 보장한다.

연습 문제

8-1

  
/**
 *
 * 연습문제 8-1
 *
 * 7장에서 만든 리스트 펑터를 사용해서 ``product`` 함수에 [1, 2, 3, 4]가 적용된 부분 적용 함수의 리스트 만들어보자.
 * 만들어진 리스트에 여러가지 값을 넣어서 테스트해보자. 예를들어 5를 넣으면 [5, 10, 15, 20]이 되어야 한다.
 *
 */
 
 fun main() {
    val curriedProduct: (Int) -> (Int) -> Int = product.curried()
    val list = Cons(1, Cons(2, Cons(3, Cons(4, Nil))))

    val productWithList: (Int) -> FunList<Int> = { n:Int -> list.fmap(curriedProduct(n)) }
    val productWithList2: (Int) -> FunList<Int> = { n:Int -> list.fmap(curriedProduct).fmap { it(n) } }

    require(productWithList(5) == Cons(5, Cons(10, Cons(15, Cons(20, Nil)))))
    require(productWithList(10) == Cons(10, Cons(20, Cons(30, Cons(40, Nil)))))

    require(productWithList2(5) == Cons(5, Cons(10, Cons(15, Cons(20, Nil)))))
    require(productWithList2(10) == Cons(10, Cons(20, Cons(30, Cons(40, Nil)))))
}

8-2

다시 살펴보기.

  
/**
 *
 * 연습문제 8-2
 *
 * 7장에서 만든 리스트 펑터를 Applicative의 인스턴스로 만들고 테스트해보자.
 *
 */

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

interface Applicative<out A>: Functor<A> {
    fun <V> pure(value: V): Applicative<V>

    infix fun <B> apply(ff: Applicative<(A) -> B>): Applicative<B>
}

sealed class AFunList<out A>: Applicative<A> {
    companion object {
        fun <V> pure(value: V): ACons<V> = ANil.pure(value)
    }
    abstract override fun <B> fmap(f: (A) -> B): AFunList<B>
    abstract fun first(): A
    abstract fun size(): Int
    override fun <V> pure(value: V): ACons<V> = ACons(value, ANil)
    abstract override fun <B> apply(ff: Applicative<(A) -> B>): AFunList<B>
}

object ANil: AFunList<Nothing>() {
    override fun <B> fmap(f: (kotlin.Nothing) -> B): AFunList<B> = ANil
    override fun first(): Nothing = throw NoSuchElementException()
    override fun size(): Int = 0

    override fun <B> apply(ff: Applicative<(Nothing) -> B>): AFunList<B> = ANil
}

data class ACons<out T>(val head: T, val tail: AFunList<T>): AFunList<T>() {
    override fun <B> fmap(f: (T) -> B): AFunList<B> = ACons(f(head), tail.fmap(f))
    override fun first(): T = head
    override fun size(): Int = tail.size() + 1

    override fun <B> apply(ff: Applicative<(T) -> B>): AFunList<B> = when(ff) {
        is ACons -> ACons(ff.head(head), tail.apply(ff))
        else -> ANil
    }
}

fun main() {
    require(AFunList.pure(1) == ACons(1, ANil))

    require(AFunList.pure(1).fmap { it * 10 } == ACons(10, ANil))
    require(ANil.fmap { a: Int -> a * 10 } == ANil)

    require(AFunList.pure(1).fmap { it * 10 } == ACons(10, ANil))
    require(ANil.fmap { a: Int -> a * 10 } == ANil)

    require(AFunList.pure(1) apply AFunList.pure { x: Int -> x * 10 } == ACons(10, ANil))
    require(ANil apply AFunList.pure { x: Int -> x * 10 } == ANil)

    require(ACons(1, ACons(2, ACons(3, ACons(4, ANil)))) apply AFunList.pure { x: Int -> x * 10 } ==
            ACons(10, ACons(20, ACons(30, ACons(40, ANil)))))
}

8-3

  
/**
 *
 * 연습문제 8-3
 *
 * 펑터를 상속받은 리스트를 만들고, ``pure``와 ``apply``를 확장 함수로 작성해서 리스트 애플리케이티브 펑터를 만들고 테스트해보자.
 *
 * 힌트 : list 2개를 합치는 확장함수 append를 만들어서 활용하라. ``FunList``의 기본 틀은 아래와 같다.
 */

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class FunList<out A>: Functor<A> {
    abstract override fun <B> fmap(f: (A) -> B): FunList<B>
    companion object
}

object Nil: FunList<Nothing>() {
    override fun <B> fmap(f: (kotlin.Nothing) -> B): FunList<B> = Nil
}

data class Cons<out T>(val head: T, val tail: FunList<T>): FunList<T>() {
    override fun <B> fmap(f: (T) -> B): FunList<B> = Cons(f(head), tail.fmap(f))
}

fun <A> FunList.Companion.pure(value: A): FunList<A> = Cons(value, Nil)

/*
ex)
this = Cons(1, Cons(2, Cons(3, Nil))), other = Cons(4, Cons(5, Cons(6, Nil))
Cons(1, Cons(2, Cons(3, Nil))).append(Cons(4, Cons(5, Cons(6, Nil))))
Cons(1, Cons(2, Cons(3, Nil)).append(Cons(4, Cons(5, Cons(6, Nil)))))
Cons(1, Cons(2, Cons(3, Nil).append(Cons(4, Cons(5, Cons(6, Nil))))))
Cons(1, Cons(2, Cons(3, Nil.append(Cons(4, Cons(5, Cons(6, Nil)))))))
Cons(1, Cons(2, Cons(3, Cons(4, Cons(5, Cons(6, Nil))))))
 */
infix fun <A> FunList<A>.append(other: FunList<A>):FunList<A> = when(this) {
    is Nil -> other
    is Cons -> Cons(head, tail.append(other))
}

/*
ex)
this = FunList.pure { x -> x * 3 }, f = Cons(1, Cons(2, Cons(3, Cons(4, Nil)))
(Cons(1, Cons(2, Cons(3, Cons(4, Nil))).fmap { x -> x * 3 }) append (Nil apply Cons(1, Cons(2, Cons(3, Cons(4, Nil))))
Cons(3, Cons(6, Cons(9, Cons(12, Nil))) append Nil
Cons(3, Cons(6, Cons(9, Cons(12, Nil)))
 */

infix fun <A, B> FunList<(A) -> B>.apply(f: FunList<A>):FunList<B> = when(this) {
    is Nil -> Nil
    is Cons -> {
        f.fmap(head) append (tail apply f)
    }
}

private fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R =
    { p1: P1 -> { p2: P2 -> this(p1, p2) } }

fun main() {
    val funList: FunList<(Int) -> Int> = FunList.pure { x -> x * 3 }
    require(funList apply Cons(1, Cons(2, Cons(3, Cons(4, Nil))))
            ==
            Cons(3, Cons(6, Cons(9, Cons(12, Nil)))))

    val funList2: FunList<(Int) -> Int> =
        Cons({ it * 3 },
            Cons({ it * 10 },
                Cons<(Int) -> Int>({ it - 2 }, Nil)))

    require(funList2 apply Cons(1, Cons(2, Cons(3, Nil)))
            ==
            Cons(3, Cons(6, Cons(9,
                Cons(10, Cons(20, Cons(30,
                    Cons(-1, Cons(0, Cons(1, Nil))))))))))

    val funList3: FunList<(Int) -> Int> = Nil
    require(funList3 apply Cons(1, Cons(2, Cons(3, Cons(4, Nil)))) == Nil)

    val funList4: FunList<(Int) -> (Int) -> Int> = FunList.pure(
        { x: Int, y: Int -> x + y }.curried())
    require(
        funList4
                apply Cons(1, Cons(2, Cons(3, Nil)))
                apply Cons(1, Cons(2, Cons(3, Nil)))
                ==
                Cons(2, Cons(3, Cons(4,
                    Cons(3, Cons(4, Cons(5,
                        Cons(4, Cons(5, Cons(6, Nil))))))))))
}

8-4

  
/**
 *
 * 연습문제 8-4
 *
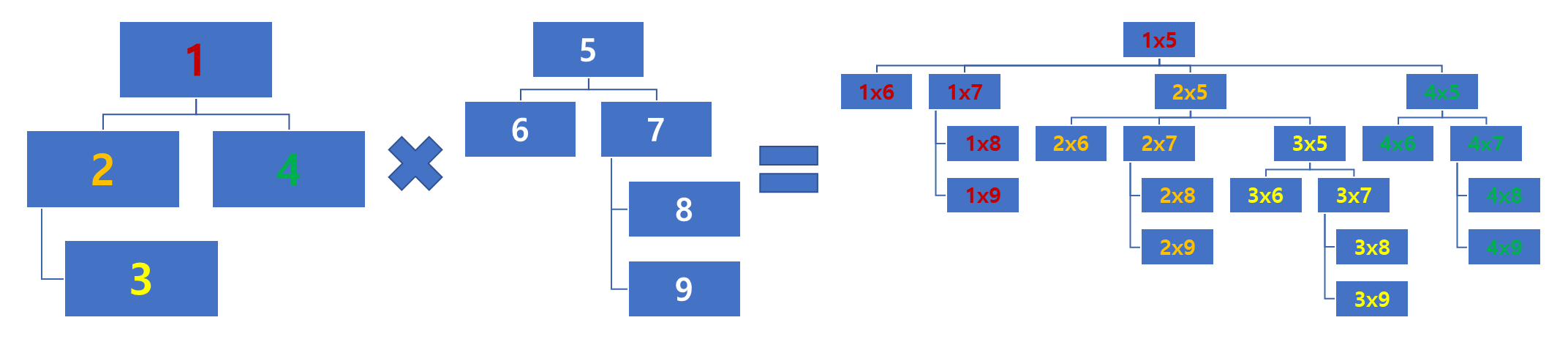
 * 아래와 같이 두 트리를 반대의 순서로 적용했을때는 어떤 트리가 완성될지 예상해보고, 테스트해보자.
 *
 */
 
fun main() {
    val tree: Tree<Int> = Node(4, listOf(Node(8), Node(12),
        Node(5, listOf(Node(10), Node(15))),
        Node(6, listOf(Node(12), Node(18)))))
    
    require(tree == Tree.pure({ x: Int, y: Int -> x * y }.curried())
            apply Node(4, listOf(Node(5), Node(6)))
            apply Node(1, listOf(Node(2), Node(3)))
    )
}

8-5

  
/**
 *
 * 연습문제 8-5
 *
 * 아래 두 트리를 apply로 결합한 트리를 프로그램으로 만들어보고, 결과가 맞는지 확인해보자.
 * Node(1, listOf(Node(2, listOf(Node(3))), Node(4, listOf())))
 * Node(5, listOf(Node(6), Node(7, listOf(Node(8), Node(9)))))
 */

fun main() {
    val treeR: Tree<Int> = Node(5, listOf(Node(6), Node(7, listOf(Node(8), Node(9))),
        Node(10, listOf(Node(12), Node(14, listOf(Node(16), Node(18))),
            Node(15, listOf(Node(18), Node(21, listOf(Node(24), Node(27))))))),
        Node(20, listOf(Node(24), Node(28, listOf(Node(32), Node(36)))))))
    require(treeR == Tree.pure({x: Int, y: Int -> x * y}.curried()) apply Node(1, listOf(Node(2, listOf(Node(3))), Node(4))) apply Node(5, listOf(Node(6), Node(7, listOf(Node(8), Node(9))))))
}

8-6

  
/**
 *
 * 연습문제 8-6
 *
 * 연습문제를 통해서 작성한 두 리스트를 ``apply`` 함수로 적용하면 모든 가능한 조합의 리스트가 반환 된다는 것을 확인했다.
 * 이번에는 리스트의 동일한 위치의 함수와 값끼리 적용되는 ZipList 애플리케이티브 펑터를 만들고 테스트해보자.
 * 단, 두 리스트의 길이가 다른 경우, 반환되는 리스트는 둘 중 짧은 리스트의 길이와 같다.
 * 예를들어, ``[(*5), (+10)]``와 ``[10, 20, 30]``을 적용하면 ``[50, 30]``이 반환될 것이다.
 *
 */
 
fun <A, B>FunList<(A)->B>.zipList(other: FunList<A>): FunList<B> = when(this) {
    is Nil -> Nil
    is Cons -> when(other) {
        is Nil -> Nil
        is Cons -> Cons(this.head(other.head), this.tail.zipList(other.tail))
    }
}

fun main() {
    val list1: FunList<(Int) -> Int> = Cons({ x :Int-> x * 5 }, Cons<(Int)-> Int>({ x: Int -> x + 10 } , Nil))
    val list2: FunList<Int> = Cons(10, Cons(20, Cons(30, Nil)))

    require(list1.zipList(list2) == Cons(50, Cons(30, Nil)))
}

8-7

  
/**
 *
 * 연습문제 8-7
 *
 * 연습문제를 통해서 작성한 두 리스트를 ``apply`` 함수로 적용하면 모든 가능한 조합의 리스트가 반환 된다는 것을 확인했다.
 * 이번에는 리스트의 동일한 위치의 함수와 값끼리 적용되는 ZipList 애플리케이티브 펑터를 만들고 테스트해보자.
 * 단, 두 리스트의 길이가 다른 경우, 반환되는 리스트는 둘 중 짧은 리스트의 길이와 같다.
 * 예를들어, ``[(*5), (+10)]``와 ``[10, 20, 30]``을 적용하면 ``[50, 30]``이 반환될 것이다.
 *
 */
 
fun <A, B>FunList<(A)->B>.zipList(other: FunList<A>): FunList<B> = when(this) {
    is Nil -> Nil
    is Cons -> when(other) {
        is Nil -> Nil
        is Cons -> Cons(this.head(other.head), this.tail.zipList(other.tail))
    }
}

fun main() {
    val list1: FunList<(Int) -> Int> = Cons({ x :Int-> x * 5 }, Cons<(Int)-> Int>({ x: Int -> x + 10 } , Nil))
    val list2: FunList<Int> = Cons(10, Cons(20, Cons(30, Nil)))

    require(list1.zipList(list2) == Cons(50, Cons(30, Nil)))
}

8-9

  
/**
 *
 * 연습문제 8-9
 *
 * 연습문제 8-3 에서 만든 리스트 애플리케이티브 펑터가 준동형 사상 법칙을 만족하는지 확인해보자.
 *
 */

fun main() {
    val function = { x: Int -> x * 2 }
    val x = 100
    require(FunList.pure(function) apply FunList.pure(x) == FunList.pure(function(x)))
}

8-10

  
/**
 *
 * 연습문제 8-10
 *
 * 연습문제 8-3 에서 만든 리스트 애플리케이티브 펑터가 교환 법칙을 만족하는지 확인해보자.
 *
 */
 
 fun <T, R> of(value: T) = { f: (T) -> R -> f(value) }
 
fun main() {
    val af1 = Cons({ x: Int -> x + 2}, Cons({ x: Int -> x + 3}, Nil))
    
    require(af1 apply FunList.pure(x) == FunList.pure(of<Int, Int>(x)) apply af1)
}

8-11

  
/**
 *
 * 연습문제 8-11
 *
 * 연습문제 8-3 에서 만든 리스트 애플리케이티브 펑터가 ``pure(function) apply af = af.fmap(function)``를 만족하는지 확인해보자.
 *
 */

fun main() {
    val function = { x: Int -> x * 2 }
    val af = Cons(1, Cons(2, Cons(3, Nil)))

    require(FunList.pure(function) apply af == af.fmap(function))
}

8-12

  
/**
 *
 * 연습문제 8-12
 *
 * AFunList 에도 동작하는 ``liftA2`` 함수를 추가해보자.
 *
 */
 
interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

interface Applicative<out A>: Functor<A> {
    fun <V> pure(value: V): Applicative<V>

    infix fun <B> apply(ff: Applicative<(A) -> B>): Applicative<B>
}

sealed class AFunList<out A>: Applicative<A> {
    companion object {
        fun <V> pure(value: V): ACons<V> = ANil.pure(value)
    }
    abstract override fun <B> fmap(f: (A) -> B): AFunList<B>
    override fun <V> pure(value: V): ACons<V> = ACons(value, ANil)
    abstract override fun <B> apply(ff: Applicative<(A) -> B>): AFunList<B>
}

object ANil: AFunList<Nothing>() {
    override fun <B> fmap(f: (Nothing) -> B): AFunList<B> = ANil
    override fun <B> apply(ff: Applicative<(Nothing) -> B>): AFunList<B> = ANil
}

data class ACons<out T>(val head: T, val tail: AFunList<T>): AFunList<T>() {
    override fun <B> fmap(f: (T) -> B): AFunList<B> = ACons(f(head), tail.fmap(f))
    override fun <B> apply(ff: Applicative<(T) -> B>): AFunList<B> = when(ff) {
        is ACons -> ACons(ff.head(head), tail.apply(ff))
        else -> ANil
    }
}

infix fun <A> AFunList<A>.append(other: AFunList<A>):AFunList<A> = when(this) {
    is ANil -> other
    is ACons -> ACons(head, tail.append(other))
}

infix fun <A, B> AFunList<(A) -> B>.apply(f: AFunList<A>):AFunList<B> = when(this) {
    is ANil -> ANil
    is ACons -> f.fmap(head) append (tail apply f)
}

private fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R = { p1:P1 -> { p2:P2 -> this(p1, p2)}}

private fun <P1, P2, R> liftA2(binaryFunction: (P1, P2) -> R): (AFunList<P1>, AFunList<P2>) -> AFunList<R> = { f1: AFunList<P1>, f2: AFunList<P2> -> AFunList.pure(binaryFunction.curried()) apply f1 apply f2  }

fun main() {
    val lifted = liftA2 { x: Int, y: Int -> x + y }
    require(lifted(ACons(1, ANil), ACons(2, ANil)) == ACons(3, ANil))

    val lifted2 = liftA2 { x: String, y: String -> x + y }
    require(lifted2(ACons("Hello, ", ANil), ACons("Kotlin", ANil)) == ACons("Hello, Kotlin", ANil))

    val lifted3 = liftA2 { x: Int, y: String -> x.toString() + y }
    require(lifted3(ACons(10, ANil), ACons("Kotlin", ANil)) == ACons("10Kotlin", ANil))

    require(lifted3(ACons(10, ACons(20, ANil)), ACons("Hello, ", ACons("Kotlin", ANil))) ==
            ACons("10Hello, ", ACons("10Kotlin", ACons("20Hello, ", ACons("20Kotlin", ANil)))))
}

8-13

  
/**
 *
 * 연습문제 8-13
 *
 * Tree 에도 동작하는 ``liftA2`` 함수를 추가해보자.
 *
 */
 
private fun <A, B, R> liftA2(binaryFunction: (A, B) -> R): (Node<A>, Node<B>)-> Node<R> = { f1: Node<A>, f2: Node<B> -> Tree.pure(binaryFunction.curried()) apply f1 apply f2 }

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class Tree<out A> : Functor<A> {

    abstract override fun <B> fmap(f: (A) -> B): Functor<B>

    companion object
}


data class Node<out A>(val value: A, val forest: List<Node<A>> = emptyList()) : Tree<A>() {

    override fun toString(): String = "$value $forest"

    override fun <B> fmap(f: (A) -> B): Node<B> = Node(f(value), forest.map { it.fmap(f) })
}

fun <A> Tree.Companion.pure(value: A) = Node(value)

infix fun <A, B> Node<(A) -> B>.apply(node: Node<A>): Node<B> = Node(
    value(node.value),
    node.forest.map { it.fmap(value) } + forest.map { it.apply(node) }
)

private fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R = { p1:P1 -> { p2:P2 -> this(p1, p2)}}

fun main() {

    val lifted = liftA2 { x: Int, y: Int -> x + y }
    require(lifted(Node(1), Node(2)) == Node(3))

    val lifted2 = liftA2 { x: String, y: String -> x + y }
    require(lifted2(Node("Hello, "), Node("Kotlin")) == Node("Hello, Kotlin"))

    val lifted3 = liftA2 { x: Int, y: String -> x.toString() + y }
    require(lifted3(Node(10), Node("Kotlin")) == Node("10Kotlin"))
}

8-14

  
/**
 *
 * 연습문제 8-14
 *
 * Either 에도 동작하는 ``liftA2`` 함수를 추가해보자.
 *
 */

private fun <A, B, R> liftA2(binaryFunction: (A, B) -> R): (Either<Nothing, A>, Either<Nothing, B>) -> Either<Nothing, R> = { f1: Either<Nothing, A>, f2: Either<Nothing, B> -> Either.pure(binaryFunction.curried()) apply  f1 apply f2 }

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class Either<out L, out R> : Functor<R> {

    abstract override fun <R2> fmap(f: (R) -> R2): Either<L, R2>

    companion object
}

data class Left<out L>(val value: L) : Either<L, kotlin.Nothing>() {

    override fun toString(): String = "Left($value)"

    override fun <R2> fmap(f: (kotlin.Nothing) -> R2): Either<L, R2> = this

}

data class Right<out R>(val value: R) : Either<kotlin.Nothing, R>() {

    override fun toString(): String = "Right($value)"

    override fun <R2> fmap(f: (R) -> R2): Either<kotlin.Nothing, R2> = Right(f(value))
}

fun <A> Either.Companion.pure(value: A) = Right(value)

infix fun <L, A, B> Either<L, (A) -> B>.apply(f: Either<L, A>): Either<L, B> = when (this) {
    is Left -> this
    is Right -> f.fmap(value)
}

private fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R = { p1:P1 -> { p2:P2 -> this(p1, p2)}}

fun main() {

    val lifted = liftA2 { x: Int, y: Int -> x + y }
    require(lifted(Right(1), Right(2)) == Right(3))

    val lifted2 = liftA2 { x: String, y: String -> x + y }
    require(lifted2(Right("Hello, "), Right("Kotlin")) == Right("Hello, Kotlin"))

    val lifted3 = liftA2 { x: Int, y: String -> x.toString() + y }
    require(lifted3(Right(10), Right("Kotlin")) == Right("10Kotlin"))
}

8-15

  
/**
 *
 * 연습문제 8-15
 *
 * ``listA3`` 함수를 구현해보자. 이 함수는 삼항 함수를 받아서 세개의 애플리케이티브 펑터를 적용하는 승격 함수다.
 *
 */
 
interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class Maybe<out A>: Functor<A> {
    abstract override fun <B> fmap(f: (A) -> B): Maybe<B>
    companion object
}

fun <A> Maybe.Companion.pure(value: A) = Just(value)

data class Just<out A>(val value: A): Maybe<A>() {
    override fun <B> fmap(f: (A) -> B): Maybe<B> = Just(f(value))
}

object Nothing: Maybe<kotlin.Nothing>() {
    override fun <B> fmap(f: (kotlin.Nothing) -> B): Maybe<B> = Nothing
}

fun <P1, P2, P3, R>((P1, P2, P3) -> R).curried(): (P1) -> (P2) -> (P3) -> R = {
    p1: P1 -> { p2:P2 -> { p3:P3 -> this(p1, p2, p3) } }
}

infix fun <A, R> Maybe<(A) -> R>.apply(f: Maybe<A>): Maybe<R> = when(this) {
    is LiftMaybe.Nothing -> LiftMaybe.Nothing
    is Just -> f.fmap(value)
}


private fun <A, B, C, R> liftA3(tripleFunction:(A, B, C) -> R): (Maybe<A>, Maybe<B>, Maybe<C>) -> Maybe<R>
        = { f1: Maybe<A>, f2: Maybe<B>, f3: Maybe<C> -> Maybe.pure(tripleFunction.curried()) apply f1 apply f2 apply f3 }

fun main() {

    val lifted = liftA3 { x: Int, y: Int, z: Int -> x + y + z }
    require(lifted(Just(1), Just(2), Just(3)) == Just(6))

    val lifted2 = liftA3 { x: String, y: String, z: String -> x + y + z }
    require(lifted2(Just("Hello, "), Just("Kotlin, "), Just("FP")) == Just("Hello, Kotlin, FP"))

    val lifted3 = liftA3 { x: Int, y: String, z: String -> x.toString() + y + z }
    require(lifted3(Just(10), Just("Hello, "), Just("Kotlin")) == Just("10Hello, Kotlin"))
}

8-16

  
/**
 *
 * 연습문제 8-16
 *
 * FunList 에도 동작하는 ``sequenceA`` 함수를 추가하고 테스트 해보자.
 *
 */
 

private fun <T> sequenceA(listOfList: AFunList<AFunList<T>>): AFunList<AFunList<T>> = when(listOfList) {
    ANil -> ACons(ANil, ANil)
    is ACons -> AFunList.pure(cons<T>().curried()) apply listOfList.head apply sequenceA(listOfList.tail)
}

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

interface Applicative<out A>: Functor<A> {
    fun <V> pure(value: V): Applicative<V>
}

sealed class AFunList<out A>: Applicative<A> {
    companion object {
        fun <V> pure(value: V): ACons<V> = ANil.pure(value)
    }
    abstract override fun <B> fmap(f: (A) -> B): AFunList<B>
    override fun <V> pure(value: V): ACons<V> = ACons(value, ANil)
}

object ANil: AFunList<Nothing>() {
    override fun <B> fmap(f: (Nothing) -> B): AFunList<B> = ANil
}

data class ACons<out T>(val head: T, val tail: AFunList<T>): AFunList<T>() {
    override fun <B> fmap(f: (T) -> B): AFunList<B> = ACons(f(head), tail.fmap(f))
}

infix fun <A> AFunList<A>.append(other: AFunList<A>):AFunList<A> = when(this) {
    is ANil -> other
    is ACons -> ACons(head, tail.append(other))
}

infix fun <A, B> AFunList<(A) -> B>.apply(f: AFunList<A>):AFunList<B> = when(this) {
    is ANil -> ANil
    is ACons -> f.fmap(head) append (tail apply f)
}

private fun <T> cons() = { x: T, xs: AFunList<T> -> ACons(x, xs) }

fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R = { p1: P1 -> { p2: P2 -> this(p1, p2) } }

fun main() {

    val listOfList = ACons(ACons(1, ACons(2, ACons(3, ANil))), ANil)
    require(sequenceA(listOfList) ==
            ACons(
                ACons(1, ANil),
                ACons(
                    ACons(2, ANil),
                    ACons(
                        ACons(3, ANil),
                        ANil)
                )
            )
    )
}

8-17

  
/**
 *
 * 연습문제 8-17
 *
 * Tree 에도 동작하는 ``sequenceA`` 함수를 추가하고 테스트 해보자.
 *
 */
 
private fun <T> sequenceA(treeList: FunList<Node<T>>): Node<FunList<T>> = when(treeList) {
    Nil -> Node(Nil)
    is Cons -> Tree.pure(cons<T>().curried()) apply treeList.head apply sequenceA(treeList.tail)
}

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class FunList<out A> : Functor<A> {
    abstract override fun <B> fmap(f: (A) -> B): FunList<B>
}

object Nil : FunList<Nothing>() {
    override fun <B> fmap(f: (Nothing) -> B): FunList<B> = Nil
}

data class Cons<A>(val head: A, val tail: FunList<A>) : FunList<A>() {
    override fun <B> fmap(f: (A) -> B): FunList<B> = Cons(f(head), tail.fmap(f))
}

private fun <T> cons() = { x: T, xs: FunList<T> -> Cons(x, xs) }

fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R = { p1: P1 -> { p2: P2 -> this(p1, p2) } }

sealed class Tree<out A> : Functor<A> {

    abstract override fun <B> fmap(f: (A) -> B): Functor<B>

    companion object
}

data class Node<out A>(val value: A, val forest: List<Node<A>> = emptyList()) : Tree<A>() {

    override fun toString(): String = "$value $forest"

    override fun <B> fmap(f: (A) -> B): Node<B> = Node(f(value), forest.map { it.fmap(f) })
}

fun <A> Tree.Companion.pure(value: A) = Node(value)

infix fun <A, B> Node<(A) -> B>.apply(node: Node<A>): Node<B> = Node(
    value(node.value),
    node.forest.map { it.fmap(value) } + forest.map { it.apply(node) }
)

fun main() {

    val treeList: Cons<Node<Int>> = Cons(Node(1), Cons(Node(2), Cons(Node(3), Nil)))
    require(sequenceA(treeList) == Node(Cons(1, Cons(2, Cons(3, Nil)))))

    val treeList2: Cons<Node<Int>> = Cons(Node(1, listOf(Node(2), Node(3))), Cons(Node(2), Cons(Node(3), Nil)))
    require(sequenceA(treeList2) ==
            Node(Cons(1, Cons(2, Cons(3, Nil))),
                listOf(
                    Node(Cons(2, Cons(2, Cons(3, Nil)))),
                    Node(Cons(3, Cons(2, Cons(3, Nil))))
                )
            )
    )
}

8-18

  
/**
 *
 * 연습문제 8-18
 *
 * Either 에도 동작하는 ``sequenceA`` 함수를 추가하고 테스트 해보자.
 *
 */

private fun <L, R> sequenceA(eitherList: FunList<Either<L, R>>): Either<L, FunList<R>> = when(eitherList) {
    Nil -> Right(Nil)
    is Cons -> Either.pure(cons<R>().curried()) apply eitherList.head apply sequenceA(eitherList.tail)
}

interface Functor<out A> {
    fun <B> fmap(f: (A) -> B): Functor<B>
}

sealed class FunList<out A> : Functor<A> {
    abstract override fun <B> fmap(f: (A) -> B): FunList<B>
}

object Nil : FunList<Nothing>() {
    override fun <B> fmap(f: (Nothing) -> B): FunList<B> = Nil
}

data class Cons<A>(val head: A, val tail: FunList<A>) : FunList<A>() {
    override fun <B> fmap(f: (A) -> B): FunList<B> = Cons(f(head), tail.fmap(f))
}

private fun <T> cons() = { x: T, xs: FunList<T> -> Cons(x, xs) }

sealed class Either<out L, out R> : Functor<R> {

    abstract override fun <R2> fmap(f: (R) -> R2): Either<L, R2>

    companion object
}

data class Left<out L>(val value: L) : Either<L, kotlin.Nothing>() {

    override fun toString(): String = "Left($value)"

    override fun <R2> fmap(f: (kotlin.Nothing) -> R2): Either<L, R2> = this

}

data class Right<out R>(val value: R) : Either<kotlin.Nothing, R>() {

    override fun toString(): String = "Right($value)"

    override fun <R2> fmap(f: (R) -> R2): Either<kotlin.Nothing, R2> = Right(f(value))
}

fun <A> Either.Companion.pure(value: A) = Right(value)

infix fun <L, A, B> Either<L, (A) -> B>.apply(f: Either<L, A>): Either<L, B> = when (this) {
    is Left -> this
    is Right -> f.fmap(value)
}

private fun <P1, P2, R> ((P1, P2) -> R).curried(): (P1) -> (P2) -> R =
    { p1: P1 -> { p2: P2 -> this(p1, p2) } }

fun main() {

    val eitherList: Cons<Right<Int>> = Cons(Right(1), Cons(Right(2), Cons(Right(3), Nil)))
    require(sequenceA(eitherList) == Right(Cons(1, Cons(2, Cons(3, Nil)))))

    val eitherList2: Cons<Either<String, Int>> = Cons(Right(1), Cons(Left("test"), Cons(Right(3), Nil)))
    require(sequenceA(eitherList2) == Left("test"))
}

개발 책, 코틀린으로 배우는 함수형 프로그래밍

This post is licensed under CC BY 4.0 by the author.

범위

개념 정리

책에서 기억하고 싶은 내용

연습 문제

8-1

8-2

8-3

8-4

8-5

8-6

8-7

8-9

8-10

8-11

8-12

8-13

8-14

8-15

8-16

8-17

8-18

Further Reading

코틀린으로 배우는 함수형 프로그래밍

코틀린으로 배우는 함수형 프로그래밍 - 1장 함수형 프로그래밍이란?

코틀린으로 배우는 함수형 프로그래밍 - 2장 코틀린으로 함수형 프로그래밍 시작하기